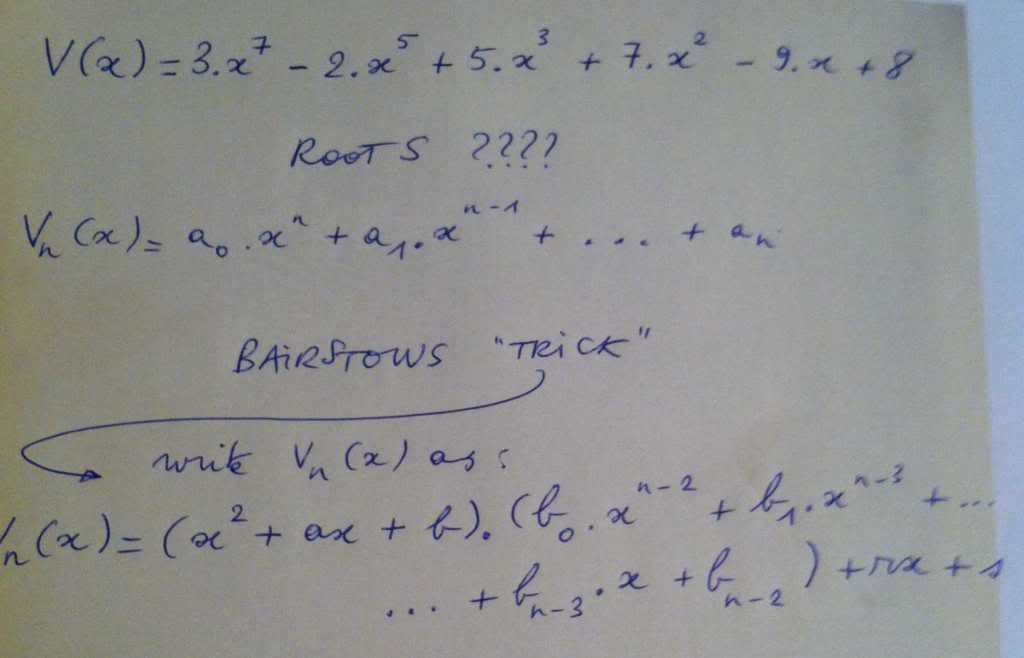SATURDAY NIGHT CRANBERRIES, BABYLON ZOO.

Cranberries with Linger.





Singer's Dolores O'Riordan.



Babylon Zoo with Spaceman.





Nite.

PROFESSOR SIR LEONARD BAIRSTOW, CBE, FRS, FRAeS (1880 – 1963).

Years ago, when I was an engineering student in Ghent, one of my favourite courses was numerical analysis. One of the first calculation and iterative methods the course covered was the Bairstow Method, named after Sir Leonard Bairstow, used to calculate the roots of a polynomial equation. Real genius often manifests itself in simple solutions, and Bairstow demonstrated this by a method which enabled to simply detach a quadratic equation off the polynomial equation! Since the roots of a quadratic equation are very simply determined, one had at the same time two roots of the larger equation, since the polynomial equation could be written as the product of the quadratic one and a polynomial one of two degrees less. So, if you put in a root of the quadratic equation, it yielded zero, but at the same time so did the product of the two equations so the roots of the quadratic one were at the same time the roots of the initial polynomial one!

It is with love that this evening, I pored once again over the notes detailing with Bairstow's Method. It looks so beautiful, I thought I wanted so share 'em, so here they are: math archaeology from the eighties:












Let me clarify; DON'T - RUN - AWAY!!!


First off, wanna see a run of the mill polynomial equation? Here it is:





Symbolically, with variables substituting for the distinct numbers above, we could write the above equation as (see the notation Vn(x) = ....):





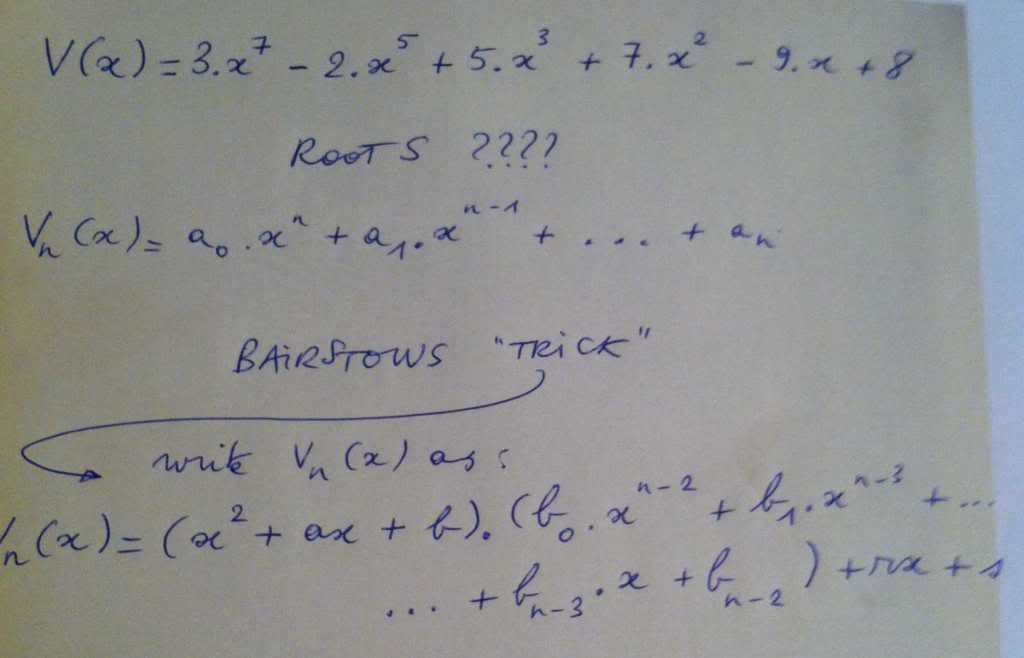
Now, as I wrote earlier, Bairstow figured that if he could just split off a quadratic equation off the bigger polynomial, and write both as a product, it would merely suffice to find the roots for the quadratic. And THAT is easy of course, in all likelihood most of you must have come across that stuff already in your third year High School:





FYI, this knowledge goes back as far as 628AD, when the Indian mathematician Brahmagupta literally described the above formula.


I consider myself lucky to have had to study numerical analysis - amongst others. If your kid has a knack for math, you might want to steer him/her into a direction in which he/she will at some point come across Bairstow and Co. Mathematics is sheer beauty. Oh, you might even give them a nod if they DON'T have that knack - I certainly didn't, but I chewed myself a way thru it and feel a better and richer person because of it.


Sir Leonard Bairstow, CBE, FRS, FRAeS (1880 – 1963), a Halifax, UK native, not only distinguished himself as a keen mathematician. Post secondary school, a scholarship secured him a place at the Royal College of Science, and once there, a Whitworth Scholarship helped him to do research into the explosion of gases. From there, he went to the National Physical Laboratory at Bushy Park where in time he became Head of aeroplane research work, holding the Zaharoff Chair of Aviation at Imperial College from 1920-1949 and becoming Professor Sir Leonard Bairstow. At some point, he also became a member of the Royal Society of London and the Royal Aeronautical Society. 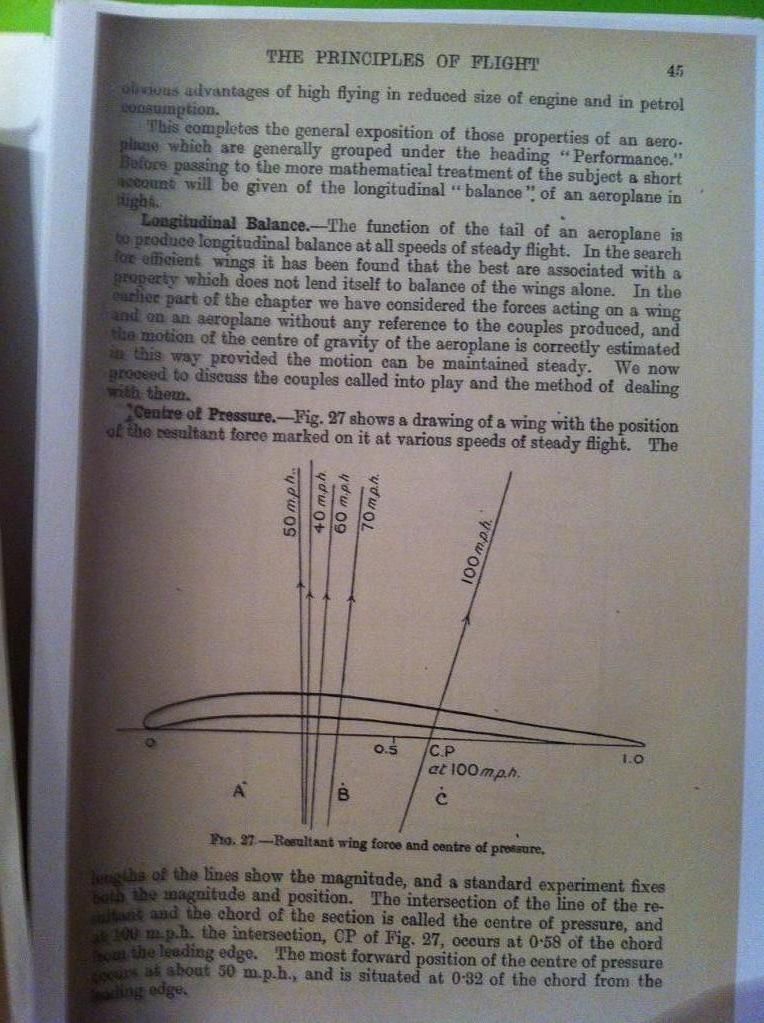While Bairstow the Mathematician established his fame with the method named after him, see above, Bairstow the Aeronatical Engineer became incontournable with his groundbreaking work Applied Aerodynamics (1920). You can download it for free, as I did (it is now a prized possession in my library), and it makes for good, if a trifle difficult reading. Good, that is, if you are an aviation enthusiast. Anyway, Applied Aerodynamics's importance at the time was so profound that it was 'field-used' into World War II and its principles hold firmly today. Below you see a pic I took of a page at random. It deals with the longitudinal balance of a plane which is determined by the couples working around its center of gravity. One of those forces is, of course, the lift produced by the speed of the aircraft. The figure shows the resultant wing force and its centre of pressure on a wing section at various speeds:





Back in those days, a work like Bairstow's was sorely needed. Without sound theoretical treatises or sufficient empirical knowledge (I'm not sure there were wind tunnels at all in the early twenties) aerodynamics was very much a business of trial and error. Test pilots paid with their lives for this, like e.g. the crew of the ill-fated Tarrant Tabor which crashed just when lifting off for its maiden flight from Farnborough on May 26, 1919:





On that day, pilot and co-pilot Captains F.G. Dunn and P.T. Rawlings, after taxying, launched Tabor F 1765, a design meant to bomb Berlin from the UK, with only the lower four engines (which were in a push pull configuration) at full throttle. At some point they also engaged the two upper engines - also at full power. You do not have to be Bairstow - you do not even have to be an aeronautical engineer - to understand what happened next. The sudden extra power of two engines placed that high above the fuselage lifted by their sheer torque the tail section up... and the nose section down. The Tabor, having just lifted off, crashed with its nose into the ground instantly killing Dunn and Rawlings.

I'm pretty sure Prof Bairstow must have been well informed about the disaster. And I'm also pretty sure that if HE had been involved in the design of the plane, he would have foreseen what happened. But it was not to be like that, and again a blood price was paid.

Bairstow himself passed away in 1963.

His research did not.





Dead White Male.



MFBB.